| 3
|
|
|
 |
|
|
| |
 1.pH
en proton concentratie 1.pH
en proton concentratie
 2.Buffers 2.Buffers
 3.Buffer
capaciteit en de effecten op de pH 3.Buffer
capaciteit en de effecten op de pH
|
|
| |
Deel
1. pH en proton concentratie
De pH is een maat voor de hoeveelheid
waterstof ionen (H+) in een oplossing: dit beïnvloedt
de oplosbaarheid van veel stoffen en de activiteit van veel biologische
systemen, van individuele moleculen tot hele organismen. Het is niet raar
als je verwacht dat een waterige oplossing losse H+ ionen (protonen)
bevat, maar dit is niet het geval. De protonen bestaan in hun gehydrateerde
vorm, als H3O+-ionen
(hydronium). De proton concentratie van een waterige oplossing
[H+] wordt door veel factoren beïnvloedt: |
|
|
| |
Veel verbindingen
gedragen zich als zuur of base: degene
die volledig geïoniseerd worden in oplossing worden meestal sterke
zuren of basen genoemd, terwijl zwakke zuren en basen maar licht worden
geïoniseerd in oplossing.
In een waterige oplossing zijn de meeste water moleculen niet
geïoniseerd. In feite is de mate van ionisatie van puur water constant
bij elke temperatuur en wordt meestal uitgedrukt
in termen van het ion produkt (of
ionisatieconstante) van water, Kw:
 Kw
= [H+][OH-] Kw
= [H+][OH-] [3.4] [3.4]
waarin [H+] en [OH-] de mol concentratie (mol
· L-1) weergeven van protonen en hydroxyl ionen in
oplossing. Bij een temperatuur van 25 ºC is het ion produkt van
zuiver water 10-14 mol2 · L-2.
Dit betekent dat de concentratie van protonen in oplossing 10-7
mol · L-1 is, met eenzelfde concentratie hydroxyl
ionen (zie [3.4]). Aangezien deze waarden erg laag zijn, is het handiger
om de pH schaal te gebruiken:
 pH = -log10[H+] pH = -log10[H+] [3.5] [3.5]
waarin [H+] de proton activiteit (= de effectieve concentratie)
is.
|
|
| |
| |
Voorbeeld:
menselijk bloed plasma heeft een
H+ concentratie van ongeveer
0.4 · 10-7 mol·L-1 (= 10-7.4
mol/L), wat een pH geeft van 7.4 |
|
|
| |
De waarde waarbij een gelijke hoeveelheid H+ en
OH- ionen aanwezig is wordt 'neutraal' genoemd:
bij een temperatuur van 25 ºC is de pH van puur neutraal water
7.0. Bij deze temperatuur zijn pH waarden beneden de 7.0 zuur en boven
de 7.0 basisch. Echter, de pH van een neutrale oplossing verandert met
de temperatuur, door de verhoogde dissociatie van water bij een toenemende
temperatuur. Wanneer de pH van een oplossing wordt gemeten en wanneer
je je resultaten gaat interpreteren moet hier dus rekening mee gehouden
worden.
Let op!: de pH is een logaritmische schaal, niet
lineair: een oplossing met een pH van 3.0 is niet twee keer zo zuur
als een oplossing met pH 6.0, maar duizend keer zo zuur (bevat dus 1000
keer zoveel H+ ionen).
Hieronder staan een aantal oefenvragen. Geef de antwoorden in 1 decimaal
nauwkeurig wanneer niet anders vermeld staat. Let hierbij op de afronding.
vb: 10.78 wordt afgerond naar 10.8 (gebruik de Angelsaksische decimaalnotatie met een punt,
dus geen 10,8). Omdat machten van 10 moeilijk te typen zijn, gebruiken
we hiervoor de volgende notatie: 4.7 10e-9 (= 4.7 · 10-9).
Let overal goed op de eenheden, bv 1.0 ml = 1.0 · 10-3
L
|
|
| |
VRAAG 1:
Wat is de pH van een oplossing met een concentratie
van 5 · 10-9 mol·L-1 protonen?
VRAAG 2:
Wat is de concentratie protonen
in een oplossing met pH 4.5? Geef het antwoord in 1 decimaal op de volgende
manier: 5.0 10e-9:
VRAAG 3:
Wat is het verschil in proton-concentratie
van oplossing A (pH = 8.3) en oplossing B
(pH = 7.8)? Geef het antwoord in 1 decimaal op de volgende
manier: 5.0 10e-9:
VRAAG 4:
Wat is het pH verschil van
oplossing A en B: oplossing A bevat 2.8 · 10-10 mol·L-1
protonen en oplossing B 8.9 · 10-5 mol·L-1
protonen?
|
| |
Deel
2. Buffers
Soms is het handiger dat je de pH ook kan controleren
i.p.v. alleen maar meten, zoals bv in een groei medium voor cellen. Eigenlijk
zou je bij elk experiment moeten overwegen om de pH te controleren, of
het nu gaat om gehele organismen, geïsoleerde cellen, sub-cellulaire
culturen of biomoleculen. Het gebruik van een buffer oplossing is één
van de meest effectieve manieren om de pH te controleren.
Definitie:
Buffer oplossing - een oplossing die een verandering in H+
concentratie (pH) door
een zuur of base kan tegengaan.
Een buffer oplossing is meestal
een mengsel van een zwak zuur en zijn geconjugeerde base. Een
stijging in protonen wordt geneutraliseerd door de anionische base terwijl
een daling in protonen, bv door toevoeging van hydroxyl ionen, wordt geneutraliseerd
door dissociatie van het zuur (zie vergelijking [3.2]);
dus het geconjugeerde paar werkt als een 'buffer' op pH veranderingen.
De weerstand van veel biologische vloeistoffen tegen pH veranderingen
wordt veroorzaakt door de aanwezigheid van cellulaire bestanddelen die
als buffer werken, zoals eiwitten die een groot aantal zwakke zure en
base groepen aan hun aminozuurketen hebben zitten.
|
| |
Deel 3. Buffercapaciteit
en de effecten op de pH
De mate van resistentie tegen de
pH veranderingen wordt de buffer capaciteit van een oplossing genoemd.
De buffer capaciteit wordt experimenteel gemeten bij een bepaalde pH door
titratie tegen een sterk zuur of base: De resulterende curve zal sterk
sigmoïdaal zijn, met een vlak waar de buffer capaciteit het grootst
is (zie figuur 3.1).
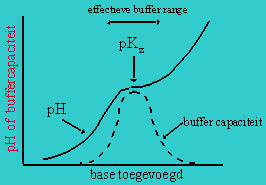 |
Figuur
3.1. Theoretische pH titratie curve van een
buffer oplossing. De pH verandering is het laagst & de buffercapaciteit
is het hoogst bij de pKz van de bufferoplossing. |
Het middenpunt van het vlak geeft de pH-waarde aan waar evenveel zuur
als geconjugeerde base aanwezig is, dit punt wordt weergegeven met het
symbool pKz, wat de negatieve logaritme van de
zuur constante, Kz, voorstelt waarvoor geldt:
 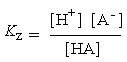 |
[3.6] vergelijk met [3.2] |
Door deze vergelijking [3.6] te om te zetten en de negatieve
logaritme te nemen, krijgen we:
|
 pH
= pKz + log 10 pH
= pKz + log 10 |
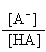 |
|
 [3.7] [3.7] |
| |
Deze relatie is bekend als de Henderson-Hasselbalch vergelijking
en het laat zien dat de pH gelijk zal zijn aan de pKz
als de verhouding van de geconjugeerde base en het zuur overeenkomstig is,
want dan is het laatste deel van de vergelijking ([3.7]) nul. Hierdoor is
de pKz van een buffer oplossing een belangrijke factor
bij bepaling van de buffercapaciteit bij een bepaalde pH. In practische
termen betekent dit dat een buffer oplossing het meest effectief werkt bij
pH waarden rond de pKz. |
| |
Kiezen van de juiste buffer oplossing
Wanneer je een buffer oplossing gaat selecteren,
moet je beseffen dat er bepaalde beperkingen aan het gebruik zitten. Citroenzuur
en fosfaat buffers vormen gemakkelijk onoplosbare complexen met divalente
cationen,
terwijl fosfaat ook kan dienen als substraat, activator
of inhibitor van bepaalde enzymen.
Beide buffers bevatten bepaalde biologische significante hoeveelheden cationen,
zoals Na+ of K+. TRIS is vaak toxisch voor biologische
systemen: door zijn hoge vet oplosbaarheid kan het membranen penetreren
waardoor het elektron transport in volledige cellen en geïsoleerde
organellen kan worden ontkoppeld.
Bepaal dus van te voren welke buffer je het beste kunt gebruiken.
|
|
Voorbeeld berekening 1. pH berekening van een zuur.
Bereken de pH van een 0.20 M HCN oplossing. De pKz
is 9.31.
Methode. Het is altijd goed om te beginnen met het opschrijven
van de chemische vergelijking en de vergelijking van de zuur constante.
Antwoord. Het evenwicht is als volgt:
|
 HCN
+ H2O HCN
+ H2O  H3O+
+ CN- H3O+
+ CN- |
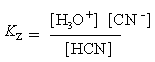 |
|
Aangezien de activiteit van de twee typen ionen
gelijk is, is [CN-] = [H3O+]. Bij dit
zwakke zuur kunnen we bovendien de verandering in [HCN] door dissociatie verwaarlozen.We herschikken
de vergelijking als volgt:
|
 [H3O+]
= [H3O+]
=
|
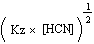 |
|
|
Door het logaritme te nemen en het teken om te zetten verkrijgen we de
volgende vergelijking:
 pH =
1/2 pKz - 1/2
log ([HCN]) pH =
1/2 pKz - 1/2
log ([HCN])
 = 1/2
× 9.31 - 1/2 log 0.20 = 5.0 = 1/2
× 9.31 - 1/2 log 0.20 = 5.0
|
| |
Voorbeeld berekening 2. pH berekening van een buffer oplossing.
Bereken de pH van een buffer oplossing die 0.100 mol·L-1
KH2PO4 en 0.200 mol·L-1
K2HPO4 bevat. De
pKz2 van H3PO4 is 7.21.
Methode. De pH van een oplossing van een zwak zuur en zijn zout
kan berekent worden aan de hand van de Henderson-Hasselbalch vergelijking.
Om dit te doen moeten we eerst het zuur HA en zijn geconjugeerde base
A- identificeren.
Antwoord. In dit voorbeeld is het zuur het anion H2PO4-
en zijn geconjugeerde base het anion HPO42-:
 H2PO4-
+ H2O H2PO4-
+ H2O  H3O+ + HPO42-
H3O+ + HPO42-
Hier is dus de pKz2 van H3PO4 voor nodig.
Dan wordt de vergelijking ([3.7]) met A- = 0.200 mol L-1
en HA = 0.100 mol·L-1 als volgt:
|
| |
 pH
= 7.21 - log pH
= 7.21 - log |
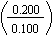
|
= |
6.91 |
| |
|
| |
Hieronder staan een
aantal oefenvragen.
|
| |
VRAAG 5:
De pKz van een zuur HA is
3.8. Een oplossing van dit zuur bevat behalve gedissociëerd zuur
nog 10 mM HA (dwz. ongesplitst zuur). Wat is de pH van deze oplossing
?
VRAAG 6:
H2CO3
dissociëert in water volgens
Kz1
Kz2
H2CO3  H+
+ HCO3- H+
+ HCO3-  2H+
+ CO32- 2H+
+ CO32-
met pKz1=3.8 ; pKz2=10.25. Wat is de pH van een
waterige oplossing die in evenwicht een concentratie van 30 mmol·L-1
H2CO3 bevat ?
VRAAG 7:
De interne pH van een spiercel is 7.2. Een belangrijke cellulaire buffer
is fosfaat. Fosforzuur (H3PO4) kan dissociëren
volgens:
Kz1 Kz2
Kz3
H3PO4  H+
+ H2PO4- H+
+ H2PO4-  2H+
+ HPO42- 2H+
+ HPO42-  3H+
+ PO43- 3H+
+ PO43-
met pKz1=2.1; pKz2=7.2; pKz3=12.7.
a) Wat is de [H 2PO 4-]/[HPO 42-]
verhouding in de cel
Via een protonenpomp
in de plasmamembraan kunnen H+ ionen vanuit de bloedbaan in
de cel gepompt worden.
b)
Wat is de concentratie H+ ionen in de cel op het moment dat
er zoveel naar binnen gepompt is dat de cellulaire pH is gedaald tot 6.2
? Geef het antwoord in de volgende vorm: 1.2 10e-8.
VRAAG 8:
Je hebt tot je beschikking 0.1 M oplossingen van NaOH, H2SO4,
azijnzuur (HA;pKz=4.8), lactaat (HL; pKz=3.8), fosforzuur
(HP; pKz=7.2), en ammoniumchloride (NH4Cl; pKz=10.3),
waarbij A-, L- en P- staan voor de betreffende
zuurresten.
a) Welke twee van de genoemde oplossingen kun
je het beste mengen om een bufferoplossing van pH=8.2 te maken ?
b) Hoeveel ml van
ieder van deze twee oplossingen moet je mengen om 100 ml van deze bufferoplossing
van pH 8.2 te maken ? Hierbij wordt geen extra water toegevoegd.
1e oplossing:
2e oplossing:
|
| |
|