Untitled Document

Chapter 10

abc-formule De abc-formule gebruik je bij het oplossen van tweede graads vergelijkingen. De abc-formule luidt als volgt:

x =	-b ± √(b² - 4ac) 2a

De a, b en c komen van : y = ax² + bx + c

In de abc-formule zit de discriminant. Deze bepaalt hoeveel oplossingen er zijn.
De D(iscriminant) = b² - 4ac
Als D>0 dan 2 oplossingen
Als D=0 dan 1 oplossing
Als D<0 dan geen oplossingen

Een voorbeeld om het duidelijk te maken: Los op: 2x² - 3x + 10 = 12

Grafisch ziet dat er zo uit:

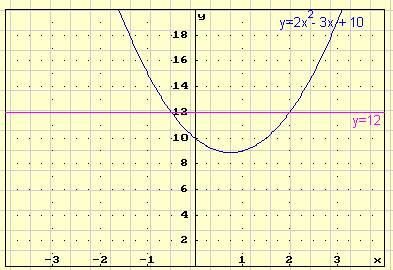
Opl:
STAP 1: eerst op 0 herleiden:
2x² - 3x +10 - 12 = 0
2x² -3x - 2 = 0

STAP 2: bepaal hoe groot a, b en c zijn:
a=2, b=-3, c=-2

STAP 3: formule invullen en uitrekenen:

x = 3 ± √((-3)² - 4.2.-2)
2.2

Dus: x = 3 ± 5
4

Dus: x = 3 + 5
4 of x = 3 - 5
4

De oplossingen zijn x = 2 of x = -½
De snijpunten zijn hier erg makkelijk want overal geldt: y = 12
Dus snijpunten (2,12) en (-½,12)

Natuurlijk zijn er ook voorbeelden te verzinnen die niet zo mooi als bovenstaand voorbeeld uitkomen. Ook daar zal ik er een van geven.

Voor welke x geldt: 3x² + x - 4 = 2x - 3

Grafisch ziet dat er zo uit:

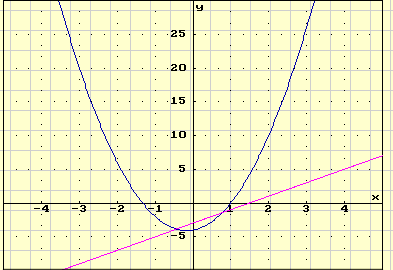
STAP 1: Op nul herleiden:
3x² + x -2x - 4 + 3 = 0
3x² - x - 1 = 0

STAP 2: a, b en c bepalen:
a = 3, b = -1, c = -1

STAP 3: invullen en uitrekenen:

x = 1 ± √((-1)² - 4.3.-1)
2.3

Dus: x = 1 ± √13
6

De oplossingen:

x = 1 + √13
6 en x = 1 - √13
6

Natuurlijk wil je ook zelf oefenen. Dat kan. Kijk hier. De antwoorden zijn ook beschikbaar!

Chapter 10