Chapter 9

Hieronder zie je de grafieken die horen bij y=sin(x), y=cos(x) en y=tan(x)

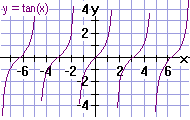
Er zijn in de goniometrie nog een aantal formules die van belang zijn.

In elke driehoek gelden de volgende regels:
sin ∠ A = cos(90° - ∠ A)
cos ∠ A = sin(90° - ∠ A)
sin² ∠ A+ cos² ∠ A = 1

tan ∠ A =

sin ∠ A cos ∠ A

Sinusregel

a  sina

=

b  sinb

=

c  sing

Cosinusregel

a² = b² + c² - 2bc.cosa

b² = c² + a² - 2ac.cosb

c² = a² + b² - 2ab.cosg

Oppervlakteregel
Opp. D ABC = ½bc sina = ½ca sinb = ½ab sing

Wat voorbeelden:

Voorbeeld 1

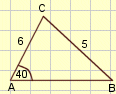Gegeven: AC=6, BC=5 en ∠ A=40° Bereken: ∠ B

Dit kun je oplossen met behulp van de sinusregel:

5  sin 40°

=

6  sinb

5 x sinb = 6 x sin 40°

sinb =

6 x sin 40° 5

b = 50°

Voorbeeld 2

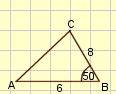Gegeven: AB=6, BC=8 en ∠ B = 50° 1) Bereken AC 2) Bereken de oppervlakte van D ABC

1) Dit kan met behulp van de cosinusregel en wel de tweede.
b² = 6² + 8² -2.8.6.cos50°
b² = 100 - 96.cos50°
b² = 38,29
b = 6,2

2) De oppervlakte berekenen met de oppevlakteregel.
Eerst goed bepalen welke je gebruiken kan!
D opp ABC = ½ca sinb
D opp ABC = ½.6.8.sin50°
D opp ABC = 18,4

Standaardhoeken
De volgende standaardhoeken moet je eigenlijk uit je hoofd kennen:
 

	0º	30º	45º	60º	90º	120º	135º	150º	180º
sin	0	0,5	½√2	½√3	1	½√3	½√2	0,5	0
cos	1	½√3	½√2	0,5	0	-0,5	-½√2	-½√3	-1
tan	0	?√3	1	√3	--	-√3	-1	-?√3	0

Chapter 9