| Chapter 15 |
Tweedegraads functies
De grafiek is een parabool. Er zijn twee soorten:
1) als a > 0 een dalparabool
2) als a < 0 een bergparabool
Let op:l Ook gedt: hoe dichter a bij 0 ligt hoe breder de parabool.
Twee voorbeelden:
Een parabool heeft een symmetrie-as. Die symmetrie-as gaat door de top en heeft als vergelijking:
| x = | -b 2a |
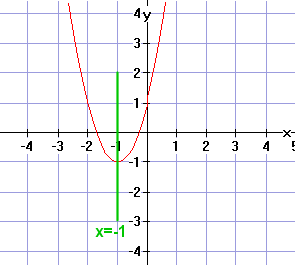
Voorbeeld:
1) dalparabool want a = 2 > 0
2) sym. as:
| x = | -4 4 |
, x = -1 |
Een tweedegraads functie zou er ook als volgt uit kunnen zien:
f : x ® a(x-p)² + q
symmetrie-as: x=p
Top (p,q)
als a > 0 een dalparabool
als a < 0 een bergparabool
Voorbeeld:
Stel een vergelijking op van een parabool met top (-4,2)
De parabool gaat door (-5,3)
Uitwerking:
1) Top invullen:
y = a(x + 4)² + 2
2) punt van parabool invullen:
(-5,3): 3 = a(-5 + 4)² + 2
3 = a + 2
a = 1
Dus vergelijking:
y = (x + 4 )² + 2
ax2 + bx + c = 0
kun je een formule afleiden waarmee je de oplossingen van zo'n vergelijking kunt uitrekenen:
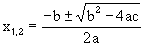
Het ± teken betekent hier niet ongeveer, maar plus of min.
Je krijgt op deze manier dus 2 antwoorden één met plus
en één met min.
In de formule speelt D = b2 - 4ac een belangrijke rol.
We noemen D de discriminant. In het algemeen is het handig om eerst
de dicriminant uit te rekenen en daarna pas de rest.
Je kunt 3 gevallen onderscheiden: